ความสูงของพีระมิด จะหาได้อย่างไร?
พีระมิดเป็นรูปหลายเหลี่ยมที่ฐานวางรูปหลายเหลี่ยม ใบหน้าทั้งหมดในรูปแบบรูปสามเหลี่ยมที่มาบรรจบกันที่จุดสูงสุดหนึ่งจุด ปิรามิดเป็นรูปสามเหลี่ยมรูปสี่เหลี่ยมและอื่น ๆ เพื่อตรวจสอบว่าพีระมิดอยู่ตรงหน้าคุณจะสามารถคำนวณจำนวนมุมที่ฐานได้ คำจำกัดความของ "พีระมิดสูง" มักพบบ่อยในปัญหาเรขาคณิตในหลักสูตรของโรงเรียน ในบทความนี้เราจะพยายามหาวิธีต่างๆในการค้นหา

ส่วนของพีระมิด
ปิรามิดแต่ละตัวประกอบด้วยองค์ประกอบต่อไปนี้:
- ใบหน้าด้านที่มีสามมุมและมาบรรจบกันที่ปลาย;
- apophema คือความสูงที่ลงมาจากปลาย;
- ด้านบนของพีระมิดเป็นจุดเชื่อมต่อขอบด้านข้าง แต่ไม่ได้อยู่ในระนาบฐาน
- ฐานเป็นรูปหลายเหลี่ยมที่ยอดไม่โกหก;
- ความสูงของพีระมิดเป็นส่วนที่ตัดด้านบนของพีระมิดและสร้างมุมฉากกับฐานของมัน
วิธีการหาความสูงของปิรามิดถ้าปริมาณของมันเป็นที่รู้จักกัน

ผ่านสูตรปริมาตรของปิรามิด V = (S * h) / 3 (inV คือปริมาตร S คือพื้นที่ฐานและ h คือความสูงของพีระมิด) เราพบว่า h = (3 * V) / S. หากต้องการแก้ไขเนื้อหาให้แก้ปัญหาได้ทันที ในรูปสามเหลี่ยมพีระมิดฐานของฐานเป็น 50 ซม2ขณะที่ปริมาตร 125 ซม3. ความสูงของพีระมิดสามเหลี่ยมไม่เป็นที่รู้จักและเราจำเป็นต้องหามัน ที่นี่ทุกอย่างง่าย: วางข้อมูลลงในสูตรของเรา เราได้รับ h = (3 * 125) / 50 = 7.5 ซม.
วิธีหาความสูงของพีระมิดหากทราบความยาวของเส้นทแยงมุมและขอบ
เท่าที่เราจำได้ความสูงของรูปปิรามิดด้วยตามมุมขวาฐาน และนั่นหมายความว่าความสูงขอบและครึ่งของเส้นทแยงมุมเข้าด้วยกันเป็นรูปสี่เหลี่ยมผืนผ้า หลายคนจำได้ว่าทฤษฎีบทของ Pythagoras รู้สองมิติค่าที่สามจะไม่ยากที่จะหา จำทฤษฎีบทที่รู้จักกันดี² = b ² + c ²ซึ่งเป็นด้านตรงข้ามและในกรณีของเราขอบของพีระมิด; b - ขาแรกหรือครึ่งหนึ่งของเส้นทแยงมุมและมี - ตามลำดับ, ขาที่สองหรือความสูงของปิรามิด จากสูตรนี้c² = a² - b²
ตอนนี้ปัญหา: ในปิรามิดที่ถูกต้องเส้นทแยงมุมเป็น 20 ซม. เมื่อเป็นความยาวของซี่โครง - 30 ซม. มันเป็นสิ่งที่จำเป็นเพื่อหาความสูง เราตัดสินใจว่า: c² = 30 ² - 20 ² = 900-400 = 500 ดังนั้น c = √ 500 = ประมาณ 22,4
วิธีหาความสูงของพีระมิดที่ตัดทอน
เป็นรูปหลายเหลี่ยมนั่นเองมีส่วนขนานไปกับฐาน ความสูงของพีระมิดตัดเป็นส่วนที่เชื่อมต่อฐานสองของ ความสูงสามารถพบได้ในพีระมิดที่ถูกต้องถ้าทราบความยาวของเส้นทแยงมุมของทั้งสองฐานรวมทั้งขอบของปิรามิด สมมติว่าเส้นทแยงมุมของฐานที่ใหญ่กว่าคือ d1 ในขณะที่เส้นทแยงมุมของฐานที่เล็กกว่าคือ d2 และขอบมีความยาว -l หากต้องการหาความสูงคุณสามารถลดความสูงบนฐานจากจุดตรงกันข้ามสองจุดบนแผนภาพ เราเห็นว่าเราได้เปิดรูปสี่เหลี่ยมผืนผ้าสองรูปสี่เหลี่ยมผืนผ้าแล้วยังคงพบความยาวของขา เมื่อต้องการทำเช่นนี้จากเส้นทแยงมุมใหญ่ให้หักค่าที่เล็กลงและหารด้วย 2 ดังนั้นเราจึงหาการตัดหนึ่งอัน: a = (d1-d2) / 2 หลังจากนั้นโดยทฤษฎีบทของ Pythagoras เราจำเป็นต้องหาขาที่สองซึ่งเป็นความสูงของพีระมิด
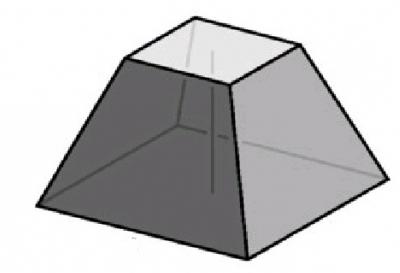
ตอนนี้ให้ดูที่สิ่งทั้งปวงนี้ในทางปฏิบัติ งานก่อนเรา ปิรามิดที่ถูกตัดทอนมีตารางที่ฐานเป็นฐานที่มากขึ้นของความยาวเส้นทแยงมุม 10 ซม. ในขณะที่มีขนาดเล็ก - 6 ซม. และครีบมีค่าเท่ากับ 4 ซม. ความสูงเป็นสิ่งจำเป็นที่จะหา .. เพื่อหาจุดเริ่มต้นของขาหนึ่ง = (10-6) / 2 = 2 ซม. ขาข้างหนึ่งจะมีค่าเท่ากับ 2 ซม. และด้านตรงข้ามมุมฉาก - 4 ซม. ปรากฎว่าสองขาหรือความสูงจะเท่ากับ 16-4 = 12 นั่นคือ H = .. √12 = ประมาณ 3.5 ซม.
</ p>




